User Tools
Sidebar
Lab AO
The Lab AO system has to roughly conjugate the pupil onto a deformable mirror. In order to see where the “pupil” is, the following diagram is useful:
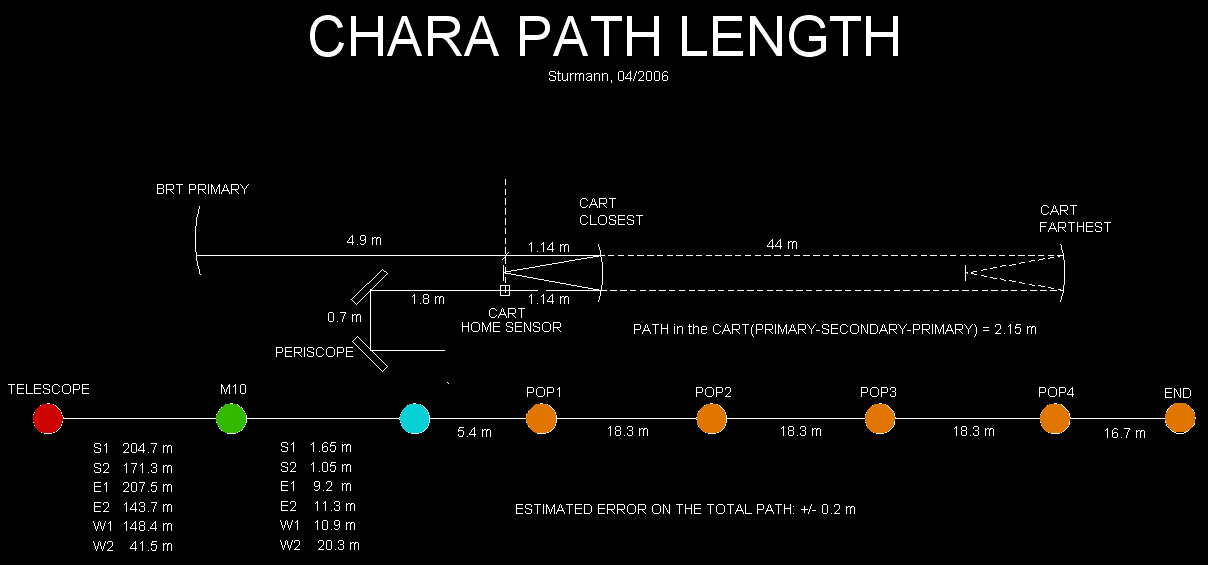
The shortest and longest distances are not realistic. e.g. W2 is essentially never used with the long POPs. A 200m distance is roughly the minimum realistic total distance from telescope to BRT primary.
The focal lengths of the CHARA BRT are:
- BRT Primary: 1280mm
- BRT Secondary: -192mm
If the BRT secondary is translated, then the beam can come to a focus, and after the focus the beam strikes in order a DM, a collimating spherical mirror, a dichroic and the LDC. The LDC shouldn't be in a converging or diverging beam. Aberrations are minimised by the BRT secondary being translated at the same time as being refocused.
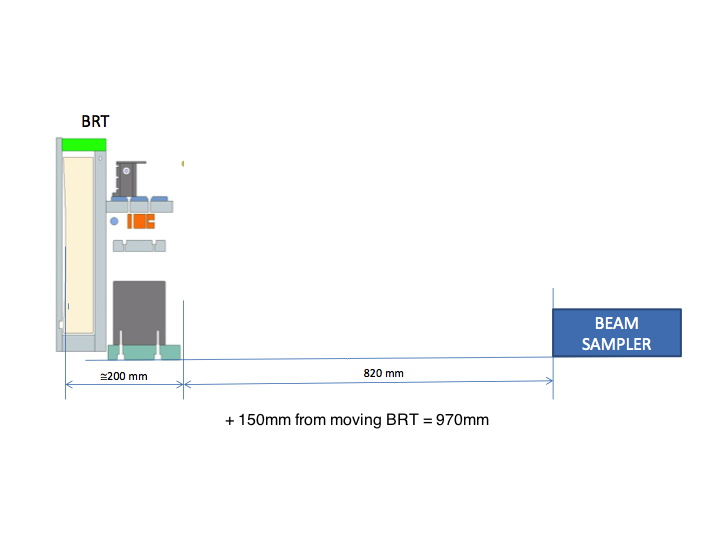
The total space from the BRT secondary to the DM is limited to somewhere in the range 2.3 to 2.45m, depending on which email from Laszlo I use. One diagram from Laszlo is below, which indicates that 1280mm + 200mm + 820mm + 150mm = 2.45m.
Working with 2.3m space and a 200m conjugation, we get the following numbers:
- BRT secondary moves towards primary by 22.9mm
- After 2300mm, an 10.5mm pupil is formed on the DM.
- After 704mm, the beam hits the collimator.
- After e.g. 300mm, the beam hits the dichroic.
- After e.g. 300mm, the beam hits the LDC
The thin-lens formula simple python script that Mike used to make these calculations is
import numpy as np import matplotlib.pyplot as plt f1 = 1280. f2 = 192. dz = 22.9#15 + np.arange(200)/10. sep = f1 - f2 + dz smallpsize=19.0 # focus_from_secondary ffs = 1.0/(1.0/(f2-dz) - 1.0/f2) #pupil distance (in mm) pd = 200000. #pupil distance to secondary pds = 1.0/(1.0/f1 - 1.0/pd) - (f1 - f2 + dz) #pupil image from secondary: pfs = 1/(1/pds - 1/f2) psize = smallpsize*(f2-dz)/f2*(pfs-ffs)/ffs #19mm collimator from pupil frat = ffs/(smallpsize*(f2-dz)/f2) colfs = ffs + smallpsize*frat colfdm = colfs - pfs #plt.plot(pfs,psize)
The wavefront sensor could be built around the 18-00079 microlens array from SUSS - 53 Euro each. These have a 30 micron pitch, meaning that with a 5 lenslet sampling across the pupil (19 lenslets altogether), the desired pupil size is 0.15mm. If there aren't enough of these in stock (SUSS are now listing these as a discontinued product), a microlens array with a different geometry may be needed. It is critical to have no more than about (focal length) * lambda * 20 > pitch^2, in order to not take up too many pixels. So an alternative is 18-00216. The catch is that this is a 10mm x 10mm piece, which ideally we'd want to be diced up.
The key is that with 3 lenses plus the microlens array, there isn't that much sensitivity loss (it is a slow wavefront sensor) and with catalog parts we can be flexible.
After the beamsplitter, towards the wavefront sensor, we need for the 30 micron pitch version:
- A 25mm diameter, 150mm focal-length achromat that forms a new pupil image.
- A 1-2mm focal-length lens to collimate, the microlens array, and a 2nd <10mm focal-length lens in a lens tube, or possibly a double
- A Thorlabs DCC1545M CMOS detector, reading out a ~320×240 subarray at >200Hz (this doesn't appear to be necessarily possible depending on computer speed, but 180Hz for 200×200 subarray is do-able).
An example Zemax for this that almost works is:
chara_oko_dm_tinyulens_140225.ZMX
chara_oko_dm_tinyulens_140225.SES
An issue with this design is that a focal-plane shift of 0.18mm is required for a 0.5 lenslet shift, because the pupil-plane is located very close to one 2mm focal-length from the 2mm lens. This both causes poor image quality and possibly vignetting, depending on how the mounts are arranged. This means that pupil alignment can not be done by tilting the beamsplitter, and the entire lens tube has to be tilted in 2 axes. Reasonably precise (~0.1mm) motion of the image-plane in front of the 2mm focal length lens is still needed, so no actuators are saved, but some tricky actuators are added.
An alternative is the Thorlabs 150 micron pitch micro lens array with square microlenses. The Zemax for this, with Mike's original configuration option is:
chara_oko_dm_ulens_140223.ZMX
The Thorlabs parts for this option without the DM mount are below:
Thorlabs - My Shopping Cart.pdf
shoppingCart.xls
The advantage of the larger micro lens arrays is that no XY translation is needed for alignment. Moving the focus spot by 130 microns moves the pupil image by 75 microns or half a lenslet. This is 180 arc sec in lab-units, or about 3 arc sec on-sky. Stability is needed at the level of 0.1 lenslets, i.e. 36 arc min, or 173 micro-radians. According to Thorlabs, this is way within spec for the mirror mount.
The z-translation of the lens tube moves the outer lenslets by 0.5 lenslets at 2.5mm, and the 0.1 lenslet tolerance is a 0.5mm motion of the lens tube. This kind of adjustment precision is possible without any z-translation mounts.
Finally - Laszlo suggested that the optical tolerances would be easier if focal-lengths were longer. This Zemax is given below, with a a shopping cart that includes both options.
chara_oko_dm_ulens_long_140226.ZMX
chara_oko_dm_ulens_long_140226.SES
Thorlabs - CHARA AO.pdf
shoppingCart-2.xls

